Problème du voyageur de commerce
Introduction du problème
On souhaite voyager dans un certain nombre de villes, tout en minimisant la distance parcourue. On a pour cela calculé la distance entre toutes les villes de notre voyage. Quel est l'itinéraire le plus court qui visite toutes les villes une et une seule fois, en revenant à la ville de départ ?
Distance | Paris | Marseille | Lyon | Toulouse | Nantes |
|---|---|---|---|---|---|
Paris | 772 | 462 | 677 | 380 | |
Marseille | 772 | 314 | 403 | 986 | |
Lyon | 462 | 314 | 537 | 681 | |
Toulouse | 677 | 403 | 537 | 585 | |
Nantes | 380 | 986 | 681 | 585 |
Définition : Problème du voyageur de commerce
Entrées :
Liste
villes: liste desnvilles à visiter.Entier
depart: numéro (indice) de la ville de départ et d'arrivée (0 <= depart < n).Liste à deux dimensions
distances: distances entre les villes (distances[i][j]indique la distance de la villevilles[i]àvilles[j]).
Sorties :
Liste chemin : chemin le plus court possible en terme de distance, qui passe par chacune des villes de
villesune unique fois, et qui commence et termine par la villedepart.
Exemple : Exemple avec quatre villes
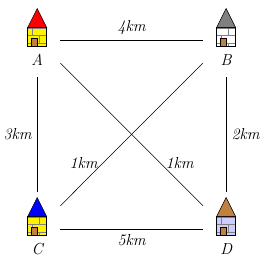
Soit les villes A, B, C et D. On donne les distances avec le schéma ci-contre. le point de départ est la ville A.
On peut trouver plusieurs chemins. Par exemple :
ABDCA de longueur \(4+2+5+3 = 14 km\).
ACBDA de longueur \(3+1+2+1 = 7 km\) qui est le plus court possible.
Complément : Nombre de chemins candidats
On peut s'intéresser aux nombres de chemins existants en fonction du nombre de villes.
Soit un problème à \(nExercice\) villes. Une ville est donnée en entrée du problème. On doit donc choisir une ville parmi les \(n-1\) villes restantes. Puis parmis les \(n-2\) villes restantes, etc.
Cela donne donc \((n-1)\times(n-2)\times(n-3)\times\dots\times2\times1=(n-1)!\) chemins candidats.
Ce nombre peut être abaissé en remarquant qu'un chemin peut être parcouru dans un sens ou dans l'autre, sans changer sa distance.
Le nombre final de chemins candidats est \(\frac{(n-1)!}{2}\).
Nombre de villes \(n\) | Nombre de chemins candidats \(\frac{(n-1)!}{2}\) |
3 | 1 |
5 | 12 |
8 | 2 520 |
10 | 181 440 |
15 | 43 589 145 600 |
Si on prend \(n=71\), alors on trouve un nombre de chemins candidats supérieur au nombre d'atomes dans l'univers.
Ce problème n'est donc pas aussi simple qu'il n'y paraît.
Remarque : Application de ce problème
Ce problème est aujourd'hui présent dans les entreprises de livraisons qui souhaitent diminuer leur temps de parcours tout en livrant au plus de personnes possibles. Avec l'arrivée des commandes en ligne, la livraison à domicile devient une course à celui qui livrera le plus vite, et donc qui optimisera son parcours.
Toutefois, il n'y a pas seulement des applications dans le domaine de la logistique, mais aussi dans le domaine de la biologie, ou de la production de circuits imprimés.
Pour en savoir plus, lire le chapitre deux de The Traveling Salesman Problem : a Computational Study.
Attention : Problèmes difficile
Ce problème est considéré comme un problème difficile, car il ne peut pas être résolu rapidement avec un grand nombre de villes (dès 12 villes, cela devient compliqué).
Il faut donc se résoudre à trouver un algorithme qui puisse s'approcher de la réponse optimale au problème sans être trop lent à s'exécuter. C'est ce que l'on appelle un algorithme glouton.