Chiffrement asymétrique
Inventé par Whitfield Diffie et Martin Hellman en 1976, le chiffrement asymétrique vient résoudre l'inconvénient essentiel du chiffrement symétrique : le nécessaire partage d'un secret (la clé) avant l'établissement de la communication sécurisée.
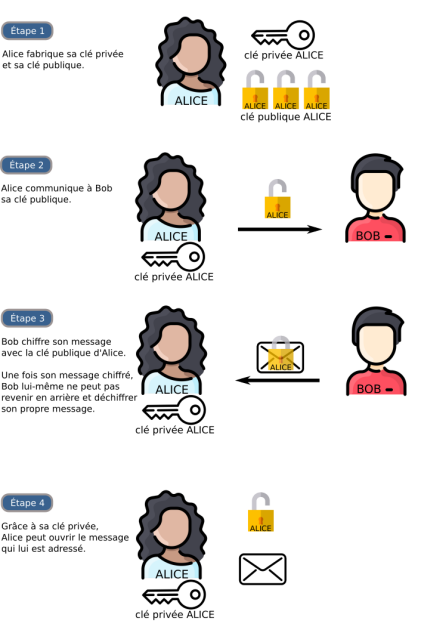
Principe
Le principe de base est l'existence d'une clé publique, appelée à être distribuée largement, et d'une clé privée, qui ne quitte jamais son propriétaire.
Le rôle interchangeable des clés publiques et privées
L'illustration précédente associe :
une image de cadenas à la clé publique (car on s'en sert pour chiffrer les messages)
une image de clé à la clé privée (car on s'en sert pour déchiffrer les messages)
Concrètement, (nous le verrons dans l'application par le chiffrement RSA), la clé privée et la clé publique sont deux nombres aux rôles identiques. Appelons-les A et B :
il est impossible de trouver A en fonction de B. Réciproquement, si on connaît A, il est impossible d'en déduire B.
si on chiffre un message avec A, on peut le déchiffrer avec B. Réciproquement, si on chiffre avec B, on peut déchiffrer le message grâce à A.
on peut donc chiffrer avec une clé publique et déchiffrer avec la clé privée associée (ce qui est fait dans l'exemple précédent). Mais on peut aussi chiffrer avec la clé privée, et déchiffrer avec la clé publique associée.
A et B ont donc des rôles interchangeables (chacun peut être un cadenas, chacun peut être une clé), et ce n'est qu'en connaissant A et B qu'on peut déchiffrer le message.
Nous allons donc maintenant adopter une nouvelle convention infographique :
Considérons ce message :

Si ce message est chiffré avec la clé publique d'Alice, le message sera :

Si on déchiffre ce message avec la clé privée d'Alice, il deviendra et donc

et donc

puisque l'application de la clé privée sur la clé publique, ou bien de la clé publique sur la clé privée, permet de retrouver le message en clair.
De manière graphique, la connaissance des deux moitiés du disque qui s'assemblent permet de les faire disparaître, peu importe qu'on ait commencé par chiffrer avec la clé publique ou avec la clé privée :  .
.

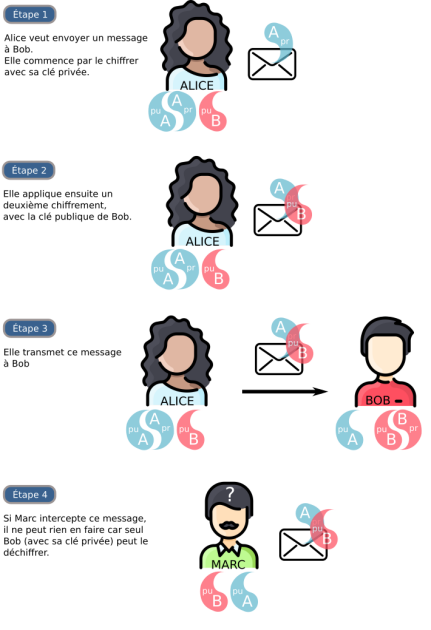
Communication authentifiée
Dans la situation précédente, Alice (qui a distribué largement sa clé publique) ne peut pas s'assurer que le message vient bien de Bob. Il peut avoir été créé par Marc, qui signe «Bob» et usurpe ainsi son identité.
Le protocole que nous allons décrire ci-dessous permet :
d'empêcher qu'un message intercepté soit déchiffré (ce qui était déjà le cas précédemment)
mais aussi de s'assurer que chaque personne est bien celle qu'elle prétend être : on résout le problème d'authentification.
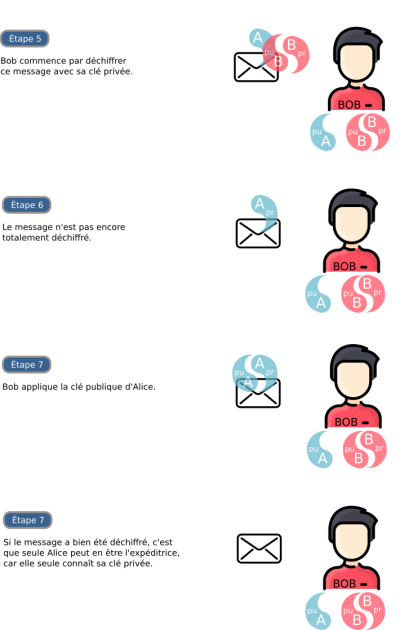
En résumé...
Alice est sûre que seul Bob pourra déchiffrer le message qu'elle envoie.
Bob est sûr que le message qu'il reçoit vient bien d'Alice.