Projet 3 : Randonnée

Présentation du projet

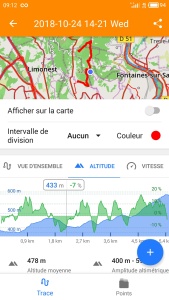
On souhaite simuler un chemin de randonnée, passant par des sommets. Le but du projet est de pouvoir simuler des temps de trajets, détecter les sommets, les dénombrer... La capture ci-contre vous donne une simulation d'une randonnée avec les dénivelés, notés sur la courbe bleue.

Le fichier à compléter est à télécharger ci-dessous.

En premier lieu, il devra être renommé sous la forme nom_prenom_projet_03.py où nom, prenom sont correctement remplacés (pas d'accent, pas d'espace, pas de majuscules).

Le docstring des fonctions ainsi que des plans de test exploitables par le module doctest sont déjà écrits, il ne faut pas les modifier !

Aperçu d'une randonnée sur l'application OsmAndInformations[1]
Projet_3_Rando_Enonce.py [py]

Remarque

Les questions 1, 2, 3 et 4 peuvent être complétées dans n'importe quel ordre.

Cependant, il faut commencer par lire l'ensemble du sujet afin de bien comprendre l'objectif.

Seul le mot-clef pass est à supprimer et à remplacer par le code de la fonction.

Attention

Tout plagiat entre élèves conduira à la note de 0 sans autre avertissement.

Question 1

Compléter le corps de la fonction test_denivele()

1
def test_denivele(tab):
2
    """
3
    tab – liste d'entiers
4
    Sortie : booléen – True si tab contient des éléments
5
             successifs distincts, False sinon.
6
    >>> test_denivele([1, 2, 3, 2, 4, 1])
7
    True
8
    >>> test_denivele([1, 2, 3, 1, 2, 2])
9
    False
10
    """

Question 2

Compléter le corps de la fonction denivele()

1
def denivele(n, mini, maxi):
2
    """
3
    n – entier strictement positif
4
    mini, maxi – entiers strictement positifs avec mini < maxi
5
    Sortie : liste – liste de n entiers aléatoires compris
6
             entre mini (inclus) et maxi (inclus). Attention,
7
             deux éléments successifs doivent être distincts.
8
    >>> test_denivele(denivele(5, 1, 4))
9
    True
10
    >>> test_denivele(denivele(20, 1, 8))
11
    True
12
    """

Dans la suite du mini-projet, on considère que la liste de nombres entiers décrit le trajet parcouru par un randonneur.

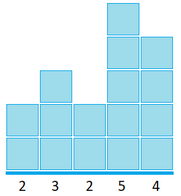
L'interprétation ci-contre illustre la liste [2, 3, 2, 5, 4].

Simulation possible d'une randonnée

Question 3

Avant de partir, le randonneur souhaite connaître le nombre de plus hauts sommets qu'il va rencontrer ainsi que leur hauteur. Avec la liste [2, 3, 2, 5, 4], il rencontre une seule fois le plus haut sommet de hauteur 5. Compléter le corps de la fonction nb_hauts_sommets().

1
def nb_hauts_sommets(chemin):
2
    """
3
    chemin – liste d'entiers dont deux éléments successifs sont
4
             distincts.
5
    Sortie : couple d'entiers – le nombre d'occurrences du plus
6
             grand élément de la liste et sa valeur.
7
    >>> nb_hauts_sommets([2, 3, 2, 5, 4])
8
    (1, 5)
9
    >>> nb_hauts_sommets([2, 8, 3, 8, 4, 8, 5, 6, 8])
10
    (4, 8)
11
    """

Question 4

Pour monter d'un niveau, le randonneur met 10 minutes. Pour descendre d'un niveau, il met 5 minutes. Ainsi, pour parcourir la liste [2, 3, 2, 5, 4], le randonneur met 50 minutes.

Compléter le corps de temps_trajet()

1
def temps_trajet(chemin):
2
    """
3
    chemin – liste d'entiers dont deux éléments successifs sont
4
             distincts.
5
    Sortie : entier – temps de parcours de la liste
6
    >>> temps_trajet([2, 3, 2, 5, 4])
7
    50
8
    >>> temps_trajet([2, 8, 3, 8, 4, 8, 5, 6, 8])
9
    240
10
    """

Question 5

Dans le programme principal, utilisez les fonctions précédentes pour simuler une randonnée.

Afficher :

  • le trajet à effectuer ;

  • le nombre de plus hauts sommets qu'il rencontrera ;

  • le temps qu'il mettra à effectuer cette randonnée.

Question 6 : BONUS

On appelle « sommet » un entier encadré par deux nombres plus petits que lui. Le premier et le dernier nombre ne peuvent donc pas être des sommets.

Concevoir une fonction qui renvoie le nombre de sommets d'un trajets. Lui ajouter un docstring complet ainsi que les tests nécessaires.