Concevoir un programme qui écrit dans un fichier nommé, MesTablesDeMultiplication.txt, l'ensemble des tables de multiplication de 1 à 10.
Ce programme utilisera with afin d'éviter à avoir à fermer le fichier. Enfin, on utilisera une fonction AjoutTable().
L'affichage final attendu, dans le fichier MesTablesDeMultiplication.txt, sera de ce type:
Table du 1 :
1*1=1
1*2=2
1*3=3
1*4=4
1*5=5
1*6=6
1*7=7
1*8=8
1*9=9
1*10=10
---------------
Table du 2 :
2*1=2
2*2=4...
A partir d'un fichier texte contenant sur chacune des lignes des nombres entiers de telle sorte :
10
50
60
70
concevoir un programme qui fait la somme de tous ces nombres.
- Une piste ?
- Encore ?
- Une analyse ?
- Solution
Il faut d'abord créer le fichier .txt avec les nombres à l'intérieur. Puis il faut
ouvrir ce fichier en lecture seule.
Nous rappellons qu'un fichier texte est une succession de lignes délimitées par un saut de ligne invisible.
La fonction read() ou write() n'utilise que le typage string. Il faudra donc transtyper...
##----- Ouverture du fichier -----##
Fichier = open('nombres.txt', 'r')
somme = 0
##----- Programme principal -----##
for ligne in Fichier:
somme += int(ligne)
##----- Affichage de la somme ----#
print(somme)
Fichier.close()
En
cliquant ici, on télécharge le texte original du «Petit Chaperon Rouge» écrit
par Carles Perrault. Ce texte est libre de droit.
Concevoir un programme qui lit le contenu de ce fichier et qui renvoie le nombre
de lettres contenues dans ce fichier, c'est-à-dire le nombre de 'a',
le nombre de 'b', le nombre de 'c',
etc... Il ne faudra tenir compte ni des espaces, ni de la ponctuation, ni des majuscules.
L'affichage final attendu sera :
Le texte contient :
220 a
27 b
59 c
79 d
415 e
26 f
47 g
36 h
180 i
7 j
0 k
168 l
74 m
156 n
157 o
94 p
34 q
190 r
136 s
238 t
175 u
59 v
0 w
10 x
9 y
7 z
- Une piste ?
- Un schéma ?
- Une analyse ?
- Solution
list('abcdefghijklmnopqrstuvwxyz')
est une instruction très intéressante pour ce programme... Pour voir ce qu'elle
réalise, n'hésitez pas à utiliser la fonction print().
On parcourt chaque ligne du fichier puis chaque caractère de chaque ligne.
Lorsque le caractère est dans la liste, on le compte.
Avoir un deuxième liste de stockage du nombre de chaque caractère semble
indispensable. Pour cela, l'instruction [0]*26
est utile et permettra d'initialiser une liste de résultats...
##----- Ouverture des fichiers -----##
fsource = open('Petit_Chaperon_Rouge.txt', 'r')
##----- Variables et constantes -----##
liste = list('abcdefghijklmnopqrstuvwxyz')
resultats = [0]*26
##----- Programme principal -----##
for ligne in fsource:
for carac in ligne:
if carac in liste:
indice = liste.index(carac)
resultats[indice] += 1
print('Le texte contient :')
for i, x in enumerate(liste):
print(resultats[i], x)
fsource.close()
Le format .pbm est un format simple d'image matricielle en noir
et blanc, c'est-à-dire formée d'un rectangle de pixels.
Une image de 10 pixels sur 10 pixels au format .pbm est tout
simplement un fichier texte contenant 10 lignes, chacune de ces lignes étant
constituée de 10 caractères '0' et/ou de
'1'. Dans ce format, chaque
'0' est interprété par un pixel blanc et
chaque '1' par un pixel noir.
Voici un exemple de script Python permettant de concevoir une image
au format .pbm :
largeur = 10
hauteur = 10
f = open('Lignes_Horizontales.pbm', 'w') # Ouverture (création) du fichier
##------ En-tête ------##
f.write('P1 \n') # P1 en ligne 1 pour déclarer le format .pbm puis passage à la ligne
f.write('{} {} \n'.format(largeur, hauteur)) # Largeur et hauteur de l'image, séparées par un espace
##------ Instructions principales ------##
for ligne in range(hauteur):
for colonne in range(largeur):
if ligne%2 == 0: # Lorsque le numéro de ligne est pair
f.write('0')
else:
f.write('1')
f.write('\n')
f.close() # Fermeture du fichier
En ouvrant ce fichier avec un éditeur de texte, on obtient l'affichage ci-dessous,
en ouvrant ce fichier avec un logiciel de visualisation d'image, on obtient l'alternance
de lignes horizontales correspondante (les pointillés bleus soulignent le tour de l'image):

P1
10 10
0000000000
1111111111
0000000000
1111111111
0000000000
1111111111
0000000000
1111111111
0000000000
1111111111
Concevoir les programmes en Python permettant d'obtenir les images
suivantes, de dimensions 150*150 :
| Un carré noir |
Colonnes noires et blanches |
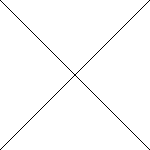
Croix sur fond blanc |
Losange noir évidé |
|---|
 |
 |
 |
 |
- Image n°1
- Image n°2
- Image n°3
- Image n°4
Pour le carré noir, tout va bien :
largeur = 150
hauteur = 150
f = open('Carre_Noir.pbm', 'w') # Ouverture (création) du fichier
##------ En-tête ------##
f.write('P1 \n') # P1 en ligne 1 pour déclarer le format .pbm puis passage à la ligne
f.write('{} {} \n'.format(largeur, hauteur)) # Largeur et hauteur de l'image, séparées par un espace
##------ Instructions principales ------##
for ligne in range(hauteur):
for colonne in range(largeur):
f.write('1')
f.write('\n')
f.close() # Fermeture du fichier
On reprend l'exemple et on teste la parité sur les numéros de colonne,
avec une petite astuce supplémentaire...
largeur = 150
hauteur = 150
f = open('Lignes_Verticales.pbm', 'w') # Ouverture (création) du fichier
##------ En-tête ------##
f.write('P1 \n') # P1 en ligne 1 pour déclarer le format .pbm puis passage à la ligne
f.write('{} {} \n'.format(largeur, hauteur)) # Largeur et hauteur de l'image, séparées par un espace
##------ Instructions principales ------##
for ligne in range(hauteur):
for colonne in range(largeur):
f.write(str(colonne%2)) # On inscrit 0 lorsque colonne est pair, 1 sinon
f.write('\n')
f.close() # Fermeture du fichier
Pour la croix, un peu de mathématiques s'imposent :
- Un pixel est sur la diagonale «descendante» lorsque son numéro
de ligne est égal à son numéro de colonne ;
- Un pixel est sur la diagonale «montante» lorsque son numéro
de ligne ajouté à son numéro de colonne donne la longueur d'un côté du carrée.
largeur = 150
hauteur = 150
f = open('Croix.pbm', 'w') # Ouverture (création) du fichier
##------ En-tête ------##
f.write('P1 \n') # P1 en ligne 1 pour déclarer le format .pbm puis passage à la ligne
f.write('{} {} \n'.format(largeur, hauteur)) # Largeur et hauteur de l'image, séparées par un espace
##------ Instructions principales ------##
for ligne in range(hauteur):
for colonne in range(largeur):
if (ligne == colonne) or (ligne+colonne == hauteur-1):
f.write('1')
else :
f.write('0')
f.write('\n')
f.close() # Fermeture du fichier
Pour le losange, ce sont les mêmes mathématiques que pour la croix,
en séparant la première de la deuxième moitié des lignes.
largeur, hauteur = 150, 150
demi = hauteur//2
f = open('Losange_Vide.pbm', 'w') # Ouverture (création) du fichier
##------ En-tête ------##
f.write('P1 \n') # P1 en ligne 1 pour déclarer le format .pbm puis passage à la ligne
f.write('{} {} \n'.format(largeur, hauteur)) # Largeur et hauteur de l'image, séparées par un espace
##------ Instructions principales ------##
for ligne in range(demi): # Parcours de la 1ère moitié des lignes
for colonne in range(largeur):
if (colonne+ligne == demi-1) or (colonne-ligne == demi-1): # 2ème diagonale du demi-carré et 1ère diagonale
f.write('1 \n')
else :
f.write('0 \n')
for ligne in range(demi): # Parcours de la 2nde moitié des lignes
for colonne in range(largeur):
if (colonne == ligne) or (colonne+ligne == largeur-1): # 1ère diagonale et 2nde diagonale
f.write('1 \n')
else :
f.write('0 \n')
f.close() # Fermeture du fichier
Images en couleur
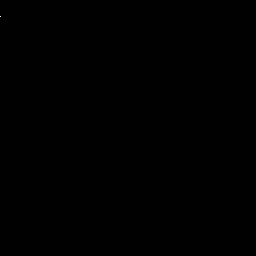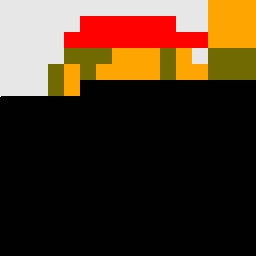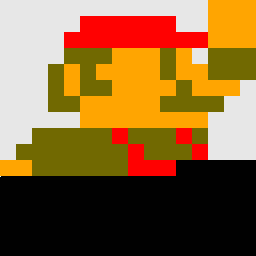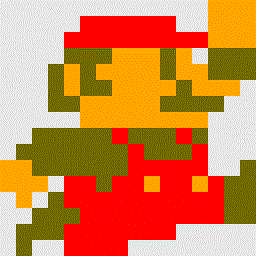
L'image ci-contre illustre la lecture linéaire (ou l'écriture) des pixels
dans une image matricielle. Pour concevoir ce type d'image, il faut donc «encoder»
les composantes de ces pixels depuis le pixel situé en haut à gauche.
Les images au format .ppm doivent comporter sur les trois premières lignes :
P3 pour encoder le fichier au format .ppm ASCII ;- la largeur puis la hauteur de l'image, séparées par un espace ;
- la valeur maximale utilisée pour estimer l'intensité maximale de chaque composante
RVB (généralement, ce sera
255).
Concevoir un programme qui permet d'obtenir l'image d'un rectangle de
100 pixels de largeur et 256
pixels de hauteur, de couleur dégradée (linéaire) du noir (en haut) vers le rouge.

Chaque pixel sera défini par sa composante RVB (Rouge, Vert, Bleu) sous forme d'un triplet R V B où
R représente la teneur en Rouge, V la teneur en Vert et B la teneur en Bleu (exemple = 100 100 100).
Essayer, ensuite, de produire d'autres dégradés plus originaux.
- Une piste ?
- Un schéma ?
- Une analyse ?
- Solution
- Variante
Le saut à la ligne compte comme un espace. Le plus intéressant est donc d'écrire :
- sur la 4ème ligne les trois composantes RVB (séparées par des
espaces) du 1er pixel ;
- sur la 5ème ligne les trois composantes RVB (séparées par des
espaces) du 2ème pixel ;
- sur la 6ème ligne les trois composantes RVB (séparées par des
espaces) du 3ème pixel ;
- etc...
La 1ère ligne comporte 100 pixels
noirs de composante '0 0 0'.
La dernière ligne comporte 100 pixels
rouges de composante '255 0 0'.
Pas d'analyse nécessaire ici.
largeur = 100
hauteur = 256
f = open('Degrade_Rouge.ppm', 'w') # Ouverture (création) du fichier
##------ En-tête ------##
f.write('P3 \n') # Format .ppm
f.write('{} {} \n'.format(largeur, hauteur)) # Largeur et hauteur de l'image, séparées par un espace
f.write('255 \n') # Maximum d'intensité des composantes
##------ Instructions principales ------##
for ligne in range(hauteur):
for colonne in range(largeur):
f.write('{} 0 0 \n'.format(ligne)) # Du noir '0 0 0' au rouge '255 0 0'
f.write('\n')
f.close() # Fermeture du fichier
Testez donc le dégradé produit par le script ci-dessous.
largeur = 100
hauteur = 256
f = open('Degrade_Original.ppm', 'w') # Ouverture (création) du fichier
##------ En-tête ------##
f.write('P3 \n') # Format .ppm
f.write('{} {} \n'.format(largeur, hauteur)) # Largeur et hauteur de l'image, séparées par un espace
f.write('255 \n') # Maximum d'intensité des composantes
##------ Instructions principales ------##
for ligne in range(hauteur):
for colonne in range(largeur):
f.write('0 {} {} \n'.format(ligne, 2*colonne))
f.write('\n')
f.close() # Fermeture du fichier
Empilement de carrés

L'image ci-contre est constituée de sept carrés de couleur noir, rouge, vert,
jaune, bleu, magenta et cyan.
- Rappeler les triplets RVB permettant de représenter les couleurs précédentes.
- Concevoir une fonction
carre(f, r, v, b) qui
permet d'ajouter au fichier f un carré de
100 pixels de côtés et de couleur unie.
- Utiliser cette fonction pour obtenir l'image ci-contre.
- Une piste ?
- Un schéma ?
- Une analyse ?
- Solution
- Variante
| Couleur |
Composante R |
Composante V |
Composante B |
|---|
| Noir |
0 |
0 |
0 |
| Rouge |
255 |
0 |
0 |
| Vert |
0 |
255 |
0 |
| Jaune |
255 |
255 |
0 |
| Bleu |
0 |
0 |
255 |
| Magenta |
255 |
0 |
255 |
| Cyan |
0 |
255 |
255 |
Pas pour cette question.
Pas pour cette question.
##----- Définition des Fonctions -----##
def carre(f, r, v, b):
"""Cette fonction ajoute au fichier f un carré de 100 pixels de côté et
de couleur unie."""
for i in range(100) :
for j in range(100) :
f.write('{0} {1} {2} \n'.format(r, v, b))
##----- Programme principal -----##
largeur = 100
hauteur = 700
f = open('Carres_Empiles.ppm', 'w') # Ouverture (création) du fichier
##------ En-tête ------##
f.write('P3 \n') # Format .ppm
f.write('{} {} \n'.format(largeur, hauteur)) # Largeur et hauteur de l'image, séparées par un espace
f.write('255 \n') # Maximum d'intensité des composantes
##------ Instructions principales ------##
carre(f, 0, 0, 0)
carre(f, 255, 0, 0)
carre(f, 0, 255, 0)
carre(f, 255, 255, 0)
carre(f, 0, 0, 255)
carre(f, 255, 0, 255)
carre(f, 0, 255, 255)
f.close() # Fermeture du fichier
Cette variante mise sur une astuce et sur la lecture des nombres binaires.
En effet,
- l'entier
0 a pour écriture binaire
'000' ;
- l'entier
1 a pour écriture binaire
'001' ;
- l'entier
2 a pour écriture binaire
'010' ;
- l'entier
3 a pour écriture binaire
'011' ;
- l'entier
4 a pour écriture binaire
'100' ;
- l'entier
5 a pour écriture binaire
'101' ;
- l'entier
6 a pour écriture binaire
'110' ;
Dans les écritures binaires ci-dessus, les '1'
sont positionnés de manière «symétrique» avec les
255 des codes RVB des couleurs utilisées pour
cette image. On définit donc une fonction binaire
qui renvoie sous forme de liste l'écriture binaire d'un entier.
##----- Définition des Fonctions -----##
def carre(f, r, v, b):
"""Cette fonction ajoute au fichier f un carré de 100 pixels de côté et
de couleur unie."""
for i in range(100) :
for j in range(100) :
f.write('{0} {1} {2} \n'.format(r, v, b))
def binaire(n):
"""Cette fonction renvoie les chiffres de l'écriture binaire "inversée"
de n sous forme de liste (le chiffre de poids k est en indice k)."""
l = []
while n!=0:
l.append(n%2)
n = n//2
while len(l)<3: # Pour avoir au minimum un triplet
l.append(0)
return l
##----- Programme principal -----##
largeur = 100
hauteur = 700
f = open('Carres_Empiles.ppm', 'w') # Ouverture (création) du fichier
##------ En-tête ------##
f.write('P3 \n') # Format .ppm
f.write('{} {} \n'.format(largeur, hauteur)) # Largeur et hauteur de l'image, séparées par un espace
f.write('255 \n') # Maximum d'intensité des composantes
##------ Instructions principales ------##
for i in range(7) : # Petite astuce : écriture binaire des nombres de 0 à 6...
triplet = binaire(i)
carre(f, 255*triplet[0], 255*triplet[1], 255*triplet[2])
f.close() # Fermeture du fichier