Pour tester ses programmes il est souvent utile de faire appel
à certaines fonctions du module random.
Exécutez plusieurs fois le programme ci-dessous afin de
bien saisir les résultats obtenus par deux d'entre elles :
Le module random
Comptons...
Cet exercice a déjà été traité dans l'Exercice n°1 de la partie Caractères. On va le généraliser en utilisant une fonction.
Définir une fonction compter()qui prend en paramètres
une chaîne de caractères et un caractère.
Cette fonction doit compter le nombre d'occurences (le nombre de fois où apparaît)
du caractère dans la chaîne.
Voici un exemple d'affichage où le programme demande à l'utilisateur d'entrer une phrase
(ci-dessous 'Ceci est un exemple.') et
un caractère (ci-dessous 'e') puis il retourne
le nombre d'occurences du carctère dans la phrase.
Entrez un phrase : Ceci est un exemple.
Entrez un caractère : e
Il y a 5 "e" dans la phrase.
Ce programme doit évidemment faire appel à la fonction compter().
Il est par contre inutile de vérifier les exceptions.
- Une piste ?
- Un schéma ?
- Une analyse ?
- Solution
compter() prend les entrées de
l'utilisateur comme paramètres et retourne un nombre qui sera affiché.
##----- Définition des Fonctions ----- ##
def compter(chaine, carac):
"""Cette fonction renvoie le nombre d'occurences du caractère carac dans chaine."""
nombre = 0 # Variable interne à la fonction qui décompte le nombre d'occurences
for lettre in chaine: # On parcourt les lettres du texte
if lettre == carac:
nombre += 1
return nombre # La fonction retourne le nombre d'occurences
##----- Programme principal ----- ##
texte = input('Entrez un phrase : ')
lettre = input('Entrez un caractère : ')
n = compter(texte, lettre)
print('Il y a {} "{}" dans la phrase.'.format(n, lettre))Le plus petit...
- Compléter la définition de la fonction
mini()qui renvoie le plus petit des deux nombres entreuetventrés en paramètres. - Le module
randomva permettre de tester cette fonction.
Dans le «Programme principal», affecter aux variablesaetbdes valeurs entières aléatoires comprises entre0et100. - Afficher la valeur stockée dans
a, celle stockée dansbpuis, en utilisant la fonctionmini(), afficher la plus petite de ces deux valeurs. - Améliorer ensuite le programme principal pour que trois
variables
a,betcprennent une valeur entière aléatoire entre1et100puis que la plus petite valeur soit affichée à l'aide de la fonctionmini().
- Une piste ?
- Solution du 1°/
- Une piste pour le 2°/
- Affichage du 3°/
- Solution du 4°/
mini()
est simple : on compare u
et v puis la
fonction renvoie la valeur du plus petit des deux
nombres.
##----- Importation des modules -----##
from random import *
##----- Définition des Fonctions -----##
def mini(u, v):
""" Entrees : deux nombres u et v
Sorties : retourne la plus petite valeur entre u et v """
if u < v:
return u
else:
return v
randint(n, p) du module
random permet de générer un entier
aléatoire compris entre les entiers n
et p (p inclus).
Par exemple, on peut obtenir l'affichage :
Entrer la valeur de a : 7 Entrer la valeur de b : 2 Ainsi, a = 2 et b = 7
##----- Importation des modules -----##
from random import *
##----- Définition des Fonctions -----##
def mini(u, v):
""" Entrees : deux nombres u et v
Sorties : retourne la plus petite valeur entre u et v """
if u < v:
return u
else:
return v
##----- Programme Principal -----##
a, b, c = randint(0,100), randint(0,100), randint(0, 100)
print('a = {}'.format(a))
print('b = {}'.format(b))
print('c = {}'.format(c))
print('Le plus petit de ces trois nombres est : {}'.format(mini(a, mini(b, c))))
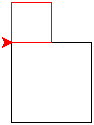
Compléter le programme ci-dessous en définissant la fonction
carre() qui prend en
arguments un crayon t, la longueur entière
cote d'un côté (en pixels) et le
sens booléen du tracé
(True pour le sens
direct).
Une fois complété, le programme conduit à l'affichage ci-contre.
- Une piste ?
- Une solution ?
- Une autre solution ?
##----- Importation des Modules -----##
from turtle import *
##----- Définition des Fonctions -----##
def carre(t, cote=40, sens=True):
""" Entrees : une tortue t, cote est un entier naturel, sens un booleen
Sorties : trace le carre de longueur cote dans le sens direct lorsque que sens=True """
for i in range(4):
t.forward(cote) # On avance
if sens == True:
t.left(90) # sens direct
else:
t.right(90)
##----- Programme principal -----##
stylo = Turtle()
carre(stylo, 80, False)
stylo.color('red')
carre(stylo)
exitonclick()
Une petite variante pour la définition de la fonction :
##----- Importation des Modules -----##
from turtle import *
##----- Définition des Fonctions -----##
def carre(t, cote=40, sens=True):
""" Entrees : une tortue t, cote est un entier naturel, sens un booleen
Sorties : trace le carre de longueur cote dans le sens direct lorsque que sens=True """
if sens: # Pourquoi cette instruction est-elle acceptable ?
angle = 90
else:
angle = -90 # Un angle négatif pour conserver la même instruction
for i in range(4):
t.forward(cote)
t.left(angle)
##----- Programme principal -----##
stylo = Turtle()
carre(stylo, 80, False)
stylo.color('red')
carre(stylo)
exitonclick()
Utiliser la fonction carre()
définie à l'exercice précédent pour tracer :
- Une suite de
10carrés de30pixels de côté espacés de10pixels.
- Le même dessin, avec une alternance.

- Une spirale de carrés espacés de
10pixels. Le carré «central» est le 1er carré tracé.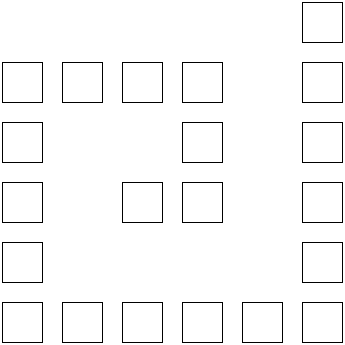
- Une piste ?
- Dessin n°1
- Dessin n°2
- Dessin n°3
##----- Importation des Modules -----##
from turtle import *
##----- Définition des Fonctions -----##
def carre(t, cote=40, sens=True):
""" Entrees : une tortue t, cote est un entier naturel, sens un booleen
Sorties : trace le carre de longueur cote dans le sens direct lorsque que sens=True """
for i in range(4):
t.forward(cote) # On avance
if sens == True:
t.left(90) # sens direct
else:
t.right(90)
##----- Tracé des 10 carrés alignés -----##
stylo = Turtle()
stylo.speed(0) # Tracé rapide !
cote = 30
espace = 10
for i in range(10):
carre(stylo, cote)
stylo.up()
stylo.forward(cote+espace)
stylo.down()
stylo.hideturtle()
exitonclick()
##----- Importation des Modules -----##
from turtle import *
##----- Définition des Fonctions -----##
def carre(t, cote=40, sens=True):
""" Entrees : une tortue t, cote est un entier naturel, sens un booleen
Sorties : trace le carre de longueur cote dans le sens direct lorsque que sens=True """
for i in range(4):
t.forward(cote) # On avance
if sens == True:
t.left(90) # sens direct
else:
t.right(90)
##----- Tracé des 10 carrés alignés -----##
stylo = Turtle()
stylo.speed(0) # Tracé rapide !
cote = 30
espace = 10
for i in range(10):
if i%2 == 0: # i est-il pair ?
carre(stylo, cote, False)
else: # ...ou impair ?
carre(stylo, cote, True)
stylo.up()
stylo.forward(cote+espace)
stylo.down()
stylo.hideturtle()
exitonclick()
##----- Importation des Modules -----##
from turtle import *
##----- Définition des Fonctions -----##
def carre(t, cote=40, sens=True):
""" Entrees : une tortue t, cote est un entier naturel, sens un booleen
Sorties : trace le carre de longueur cote dans le sens direct lorsque que sens=True """
for i in range(4):
t.forward(cote) # On avance
if sens == True:
t.left(90) # sens direct
else:
t.right(90)
##----- Tracé des 10 carrés alignés -----##
stylo = Turtle()
stylo.speed(0) # Tracé rapide !
cote = 20
espace = 10
for i in range(1, 7):
for j in range(0, i):
carre(stylo, cote)
stylo.up()
stylo.forward(cote+espace)
stylo.down()
stylo.up()
stylo.forward(cote)
stylo.left(90)
stylo.down()
stylo.hideturtle()
exitonclick()
Généraliser la fonction carre()
en définissant une nouvelle fonction
polygone(t, n=4, cote=40, sens=True)
qui, en utilisant un crayon t
du module turtle, trace un polygone régulier
à n côtés de longueur
cote dans le
sens booléen du tracé.
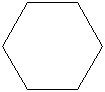
Par exemple, la figure ci-contre sera obtenue en entrant l'instruction :
polygone(stylo, 6, 50, True)
En utilisant cette fonction, essayer d'obtenir la figure ci-dessous :
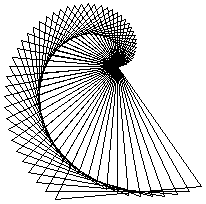
- Une piste ?
- Une autre piste ?
- Encore une piste ?
- Fonction
polygone()? - Solution pour la spirale ?
- Un triangle équilatéral a trois angles de 60° ;
- Un carré a quatre angles de 90° ;
- Un pentagone régulier a cinq angles de 108° ;
- Un polygone régulier à
ncôtés a doncnangles de ...° .
Rappel sur les déplacements :
- Avant l'instruction
.left(50):
- Après l'instruction
.left(50):
En informatique, il faut souvent utiliser les mathématiques !!!
- L'angle «extérieur» entre deux côtés consécutifs d'un triangle équilatéral est \(180 - 60 = 120°\) ;
- L'angle «extérieur» entre deux côtés consécutifs d'un carré est \(180 - 90 = 90°\) ;
- L'angle «extérieur» entre deux côtés consécutifs d'un pentagone régulier est \(180 - 108 = 72°\).
- La somme des angles d'un polygone régulier à \(n\) côtés
est \(180 \times \left(n-2\right) \).
Chacun de ces angles a donc pour mesure \( \frac {180 \times \left(n-2\right)}{n} = 180 - \frac{360}{n} \) et l'angle «extérieur» entre deux côtés consécutifs d'un polygone régulier est \(180 - \left(180 - \frac{360}{n} \right ) = \frac{360}{n} \).
##----- Importation des Modules -----##
from turtle import *
##----- Définition des Fonctions -----##
def polygone(t, n=4, cote=40, sens=True):
""" Entrees : une tortue t, n et cote sont des entiers naturels, sens un booleen
Sorties : trace le polygone regulier a n cotes de longueur cote dans le sens direct lorsque que sens=True """
if sens:
angle = 360/n
else:
angle = -360/n
for i in range(n):
t.forward(cote) # On avance
t.left(angle)
##----- Programme principal -----##
stylo = Turtle()
stylo.speed(0)
polygone(stylo, 6, 50, True)
stylo.hideturtle()
exitonclick()
##----- Importation des Modules -----##
from turtle import *
##----- Définition des Fonctions -----##
def polygone(t, n=4, cote=40, sens=True):
""" Entrees : une tortue t, n et cote sont des entiers naturels, sens un booleen
Sorties : trace le polygone regulier a n cotes de longueur cote dans le sens direct lorsque que sens=True """
if sens:
angle = 360/n
else:
angle = -360/n
for i in range(n):
t.forward(cote) # On avance
t.left(angle)
##----- Programme principal -----##
stylo = Turtle()
stylo.speed(0)
for i in range(50):
polygone(stylo, 3, 3*i, True)
stylo.left(5)
stylo.hideturtle()
exitonclick()