Graphes
Introduction aux graphes
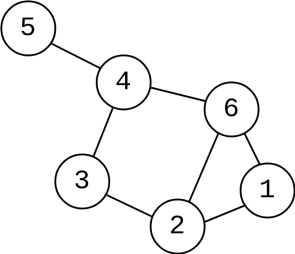
Un graphe est une structure mathématique utilisée pour modéliser des relations entre objets. Il est composé de deux éléments principaux : les sommets (ou nœuds) et les arêtes (ou liens).
Voyons ensemble les graphes, dans le cadre des réseaux sociaux.
Définition : Sommets
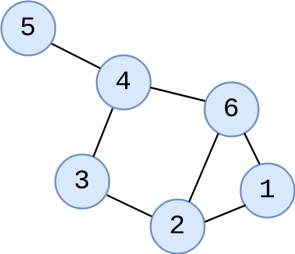
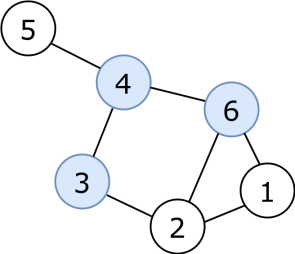
Les sommets sont les entités individuelles dans le graphe. Un sommet peut comporter une information, comme par exemple un nom, une lettre ou un numéro. Par exemple, dans un réseau social, chaque personne serait un sommet. | Graphe - Les sommets sont indiqués en bleu |
Définition : Arêtes
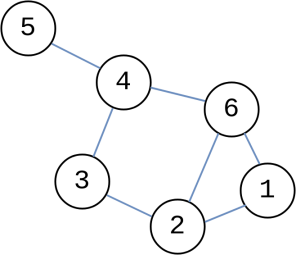
Graphe - Les arêtes sont indiquées en bleu | Les arêtes sont les connexions entre les sommets. Chaque arête est donc reliée à deux sommets. Dans l’exemple du réseau social, une arête pourrait représenter une relation d’amitié entre deux personnes. |
Définition : Voisins
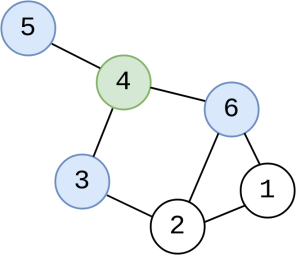
Deux sommets sont dits voisins s’ils sont reliés par une arête. Dans notre exemple de réseau social, deux personnes sont voisines si elles sont amies. | Graphe - Les voisins du sommet vert sont indiqués en bleu |
Définition : Degrés
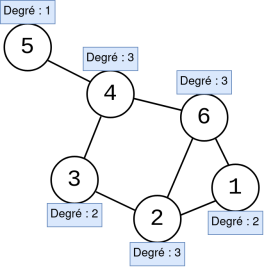
Graphe - Les degrés de chaque sommet sont indiqués en bleu | Le degré d’un sommet est le nombre d’arêtes qui lui sont connectées, autrement dit le nombre de voisins de ce sommet. Dans le contexte d’un réseau social, le degré d’une personne serait le nombre de ses amis. |
Rayon et diamètre d’un graphe
Définition : Excentricité d'un sommet
L'excentricité d'un sommet est la distance du sommet le plus éloigné. Cette distance est calculée en prenant le chemin le plus court.
Exemple :
Dans cet exemple :
|
Définition : Rayon
Le rayon d’un graphe est la plus petite excentricité parmi tous les sommets du graphe.
Définition : Diamètre
Le diamètre d’un graphe est la plus grande excentricité parmi tous les sommets du graphe.
Exemple :
Toujours dans le même exemple, le rayon est de 2, et le diamètre est de 3. |
Dans un réseau social, le rayon pourrait donner une idée de la « portée » d’une information (combien de « sauts » elle doit faire pour atteindre tout le monde).
De même, le diamètre pourrait donner une idée de la séparation maximale entre deux personnes dans le réseau.
Centre d'un graphe
Définition : Centre
Le centre d’un graphe est l’ensemble des sommets dont l’excentricité est égale au rayon du graphe. |
Dans le contexte des réseaux sociaux, le centre d’un graphe peut être interprété comme les utilisateurs les plus « centraux » ou les plus influents dans le réseau.
Ces utilisateurs sont souvent ceux qui sont les plus proches de tous les autres utilisateurs dans le réseau, ce qui signifie qu’ils peuvent diffuser des informations plus rapidement et plus efficacement à travers le réseau.
Entrainement
Réaliser l'exercice sur les graphes avant de passer à la suite.