Activité 3 : Origine de l'étude des petits mondes

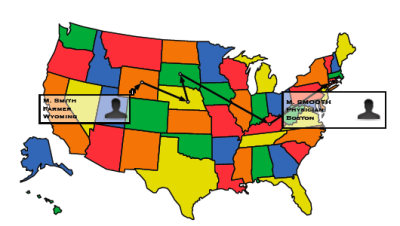
L'utilisation du terme « petit monde » remonte à l'expérience sociologique de Stanley Milgram effectuée en 1967. Il s'agissait de demander à un échantillon (supposé aléatoire) de 300 Américains du Nebraska de faire parvenir une lettre à un individu cible dont ils n'avaient pas l'adresse, mais sur lequel ils possédaient des informations (sa profession : courtier, son lieu de travail : Boston...). La règle était de ne transmettre la lettre qu'à une de ses connaissances propres.

Relativement peu de lettres sont arrivées à destination (environ un quart), mais le résultat surprenant fut que la longueur moyenne d'une chaîne de porteurs du message de son origine jusqu'à sa destination était très faible (environ 6). Pourtant, le nombre d'individus potentiellement concernés par le réseau social mis en jeu était très important (plusieurs centaines de millions), les personnes étaient éloignées géographiquement et socialement entre elles, et enfin, aucune d'elles n'avait la carte du réseau social.

Exercice d'application résolu  :

Supposons que Julia rencontre Paul. Paul lui parle de son emploi de journaliste, qu'il a obtenu grâce à un ami, Robert, qui habite Reuilly-les-Olivettes.

Julia s'étonne, car sa tante, qui habite ce village, y connaît un journaliste nommé Robert (son voisin) : « le monde est petit ! »

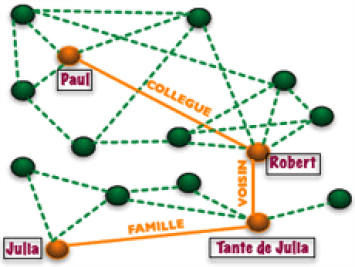
Nous avons donc le chemin suivant, de longueur 3 :

Julia —lien familial— Tante de Julia —lien de voisinage— Robert —lien professionnel— Paul.

Chemin de longueur trois reliant Julia à Paul. Le type des liens utilisés est précisé. Les liens en pointillés représentent le reste du réseau social.

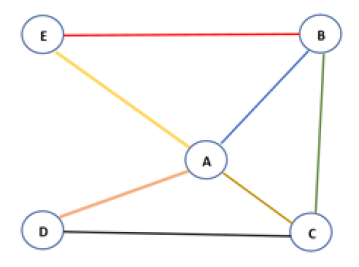
Exercice d'application à résoudre : Diamètre, centre et rayon d'un graphe

A partir du graphe suivant, compléter le tableau suivant et identifier le centre du graphe, son diamètre et son rayon.

A compléter

Distance de

A

B

C

D

E

Distance la plus grande par ligne

A

B

C

D

E

Exercice d'application à résoudre  : La représentation d'un réseau social de 6 personnes

Représenter sous forme d'un graphe, un réseau social constitué de 6 personnes A, B, C, D, E, et F où :

A est ami avec B et D

B est ami avec A, C et E

C est ami avec B et E

D est ami avec A et E

E est ami avec F

Distance de

A

B

C

D

E

F

Distance la plus grande par ligne

A

B

C

D

E

F