
Cet exemple peut correspondre à un fond de ciel d'intensité constante avec une étoile faible dont toute la luminosité est concentrée dans un seul pixel. Comment souligner la présence de cette étoile ? La réponse est d'augmenter le contraste... (voir le cas du filtre passe-haut)
Le principe du filtrage est de modifier la valeur des pixels d'une image, généralement dans le but d'améliorer son aspect. En pratique, il s'agit de créer une nouvelle image en se servant des valeurs des pixels de l'image d'origine.
Un filtre est une transformation mathématique (appelée produit de convolution) permettant de modifier la valeur d'un pixel en fonction des valeurs des pixels avoisinants, affectées de coefficients. Les calculs sont faits pour chacune des trois composantes de couleur. Le filtre est représenté par un tableau (une matrice), caractérisé par ses dimensions et ses coefficients, dont le centre correspond au pixel concerné.
Ce filtre lisseur part du principe que la valeur d'un pixel est relativement similaire à son voisinage. Il fait donc en sorte que chaque pixel est remplacé par la moyenne pondérée de ses voisins. Cela signifie qu'on additionne la valeur de tous les pixels du voisinage du pixel traité. On obtient ainsi la matrice de convolution suivante :
$$h = \frac{1}{9} \times
\begin{pmatrix}
1 &1 &1 \\
1 &1 &1 \\
1 &1 &1
\end{pmatrix}$$
$h$ s’appelle le masque de convolution. La somme des coefficients du masque valant 1, le lissage préservera toute zone de l’image où le niveau de gris est constant. Prenons ces méduses et appliquons-leur un filtre passe-bas.
Le résultat est que l'image devient plus floue, en particulier ses contours. Ce filtre peut peut engendrer des phénomènes de fausses couleurs, contrairement au filtre médian.
Une amélioration du filtre passe-bas consiste à jouer sur les valeurs des coefficients du masque : $$h = \frac{1}{10} \times \begin{pmatrix} 1 &1 &1 \\ 1 &2 &1 \\ 1 &1 &1 \end{pmatrix}$$
À l'inverse, la matrice ci-après rendra l'image plus nette. C'est un filtre passe-haut
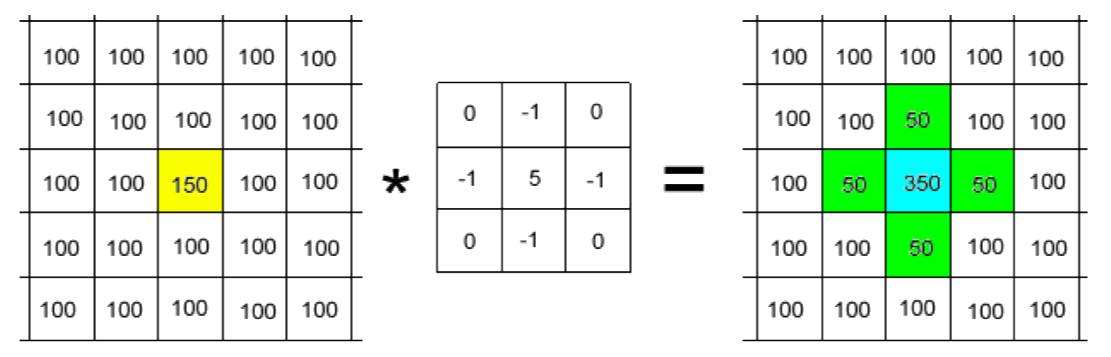
Un filtre passe-haut est caractérisé par un noyau comportant des valeurs négatives autour du pixel central. Cette accentuation peut permettre de mettre en exergue les limites entre les zones homogènes de l'image, et est alors appelée extraction de contours.
$$\begin{pmatrix}
0& -1& 0\\
-1& 5& -1\\
0& -1& 0
\end{pmatrix}$$
Toutefois, son utilisation fait apparaître certains effets indésirables :
La détection de contour est une étape préliminaire à de nombreuses applications dans le traitement d’image. Les contours constituent en effet des indices riches pour toute interprétation ultérieure de l’image.
Pour faire simple, l'opérateur calcule le gradient de l'intensité de chaque pixel. Ceci indique la direction de la plus forte variation du clair au sombre, ainsi que le taux de changement dans cette direction. On connaît alors les points de changement soudain de luminosité, correspondant probablement à des bords.
Opérateur Laplacien :
$$h = \begin{pmatrix} 0 &1 &0 \\ 1 &-4 &1 \\ 0 &1 &0 \end{pmatrix}$$Opérateur Laplacien (avec les diagonales):
$$h = \begin{pmatrix} 1 &1 &1 \\ 1 &-8 &1 \\ 1 &1 &1 \end{pmatrix}$$La technique de filtre médian est largement utilisée en traitement d'images numériques, car elle permet de réduire le bruit tout en conservant les contours de l'image.
L'idée principale du filtre médian est de remplacer chaque pixel par la valeur médiane de son voisinage.
Considérons neuf pixels en niveaux de gris, dont une valeur est aberrante (ici 255) :
| 2 | 4 | 12 |
| 2 | 255 | 3 |
| 7 | 9 | 3 |
Le filtre médian va d'abord trier ces valeurs par ordre croissant :
2, 2, 3, 3, 4, 7, 9, 12, 255
et prendre la valeur médiane (la cinquième valeur), ici la valeur 4. La sortie du filtre donnera :
| 2 | 4 | 12 |
| 2 | 4 | 3 |
| 7 | 9 | 3 |
 Elimination du bruit après 2 applications du filtre médian
Elimination du bruit après 2 applications du filtre médian
Voir ici pour l'implémentation Python du filtre médian.
Voir ici pour la correction de l'exercice 1.
Voir ici pour la correction de l'exercice 2.
La matrice déjà saisie permet le « repoussage » (effet d'embossement...).
A vous de tester vos propres matrices de convolution...