Classification
L'algorithme des k plus proches voisins résout un certain type de problème : la classification.
Définition : Problème : Classification
Un problème de classification s'exprime dans le cadres suivant :
on dispose d'un ensemble \(C\) de classes ;
on dispose d'un ensemble \(E\) d'éléments ;
chaque élément \(e\) de \(E\) est associé à une unique classe \(c(e)\) de \(C\).
Définition : Algorithme des k plus proches voisins
L'algorithme des k plus proches voisins permet de déterminer la classe \(c(e)\) de chaque élément \(e\) de \(E\) dans les cas où :
on ne peut pas facilement déterminer \(c(e)\) ;
on dispose déjà, dans une liste d'association \(L\), de valeurs correctes de \(c(e)\) pour certains \(e\) ;
on dispose d'une notion de distance dans \(E\), c'est-à-dire qu'on peut associer une valeur numérique positive entre deux éléments de \(E\).
Comme son nom l'indique, une valeur \(k\) doit être spécifiée. Il s'agit d'un entier strictement positif qui indique le nombre de voisins à considérer lors de la recherche de \(c(e)\).
Méthode : Fonctionnement de l'algorithme
L'algorithme prend donc en entrée :
un paramètre \(k\) ;
un élément \(e\) ;
une liste d'association \(L\) ;
et renvoie une classe \(c\) pour laquelle il a le plus confiance à ce que \(c(e) = c\).
Pour cela :
il regarde parmi tous les éléments \(e_i\) dans \(L\) lesquels sont les \(k\) plus proches de \(e\) ;
il consulte leur classe via L ;
il renvoie la classe c la plus présente parmi ses résultats.
Exemple : Exemple de classification
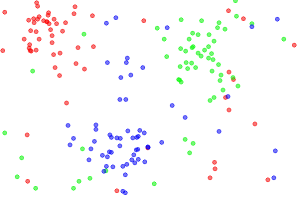
On présente ici un ensemble de données à deux dimensions déjà classifiées en trois catégories : rouge, vert et bleu.
On peut supposer que la couleur indique le lycée de rattachement de chaque élève positionné via la latitude et la longitude de leur domicile.
On s'intéresse désormais à savoir quelle valeur de k utiliser.
Une valeur faible risque de causer des erreurs dues à certaines valeurs exceptionnelles (par exemple, un rond vert avec des ronds rouges).
À l'inverse, une valeur trop élevée risque de prendre en compte des éléments trop éloignés et donc non significatifs.
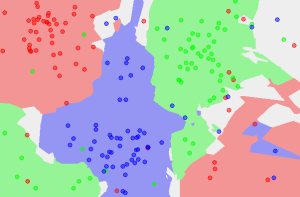
Voici ci-contre un exemple avec \(k=1\). On remarque que la valeur est trop faible !
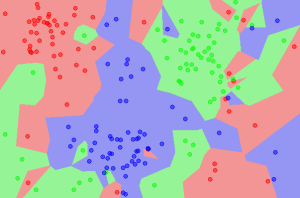
Et voici un dernier exemple avec \(k=5\). Le résultat semble déjà plus correct.
Définition : Liste d'association
Une liste d'association est un dictionnaire dont les clés sont les éléments e de E et les valeurs sont les classes c(e) de C.