Notion de distance
Comme vu précédemment, l'algorithme des k plus proches voisins repose sur la notion de distance dans un ensemble.
Définition : Distance
La distance est une fonction qui associe à deux éléments \(e_1\) et \(e_2\) de E une valeur réelle positive ou nulle en respectant quelques critères :
Si \(e_1\) et \(e_2\) sont proches, alors leur distance est proche de zéro.
Si \(e_1\) et \(e_2\) sont très différents, alors leur distance est élevée.
Si \(e_1\) et \(e_2\) sont égaux, alors leur distance est nulle.
Nous allons voir des distances de type géométrique, utilisées pour les ensembles d'éléments numériques.
Toutefois, d'autres distances existent, qui s'adaptent à tout type de données.
Distance géométrique
La distance géométrique est la distance entre deux points dans un espace à une ou plusieurs dimensions.
À une dimension, il suffit de faire la différence entre les deux points pour connaître leur distance.
Dès l'espace à deux dimensions, cela se complique.
Méthode : Distance euclidienne
La distance euclidienne est la distance en ligne droite entre deux points.
Si on dispose de deux points \(A(x_A,y_A)\) et \(B(x_B,y_B)\), alors on peut calculer leur distance euclidienne avec la formule suivante :
\(distance(A, B)=\sqrt{(x_A-x_B)^2+(y_A-y_B)^2}\)
On en déduit facilement la distance euclidienne à trois dimensions ou plus :
\(distance(A, B)=\sqrt{(x_A-x_B)^2+(y_A-y_B)^2+(z_A-z_B)^2}\) pour \(A(x_A,y_A,z_A)\) et \(B(x_B,y_B,z_B)\) (trois dimensions).
Méthode : Distance de Manhattan
La distance de Manhattan consiste à supposer qu'on ne peut pas traverser l'espace en ligne droite (comme dans la ville de Manhattan) et qu'on doit donc suivre les axes de la dimension.
Le schéma ci-contre indique une distance de Manhattan de 12 (en rouge, bleu et jaune) contre une distance euclidienne d'envrion 8 (en vert).
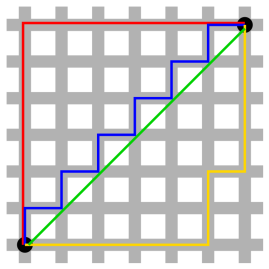
La distance de Manhattan (chemins rouge, jaune et bleu) contre la distance euclidienne en vert.
Elle se calcule facilement en faisant la différence de chaque dimension des points :
\(distance(A,B)=\left|x_A-x_B\right|+\left|y_A-y_B\right|\)
Autres distances
Si on dispose de chaînes de caractères, on peut utiliser la distance de Hamming. Cette distance indique le nombre de lettres différentes entre deux mots.
On peut également immaginer une distance entre deux mots où la distance mesure le sens des mots (par exemple, lycée et élève sont proches, mais ver et verre sont éloignés).