Lycée de secteur

Le problème

On dispose d'une liste qui associe à certaines adresses géographiques un lycée de secteur du département 31 (Haute-Garonne).

  • Les adresses sont en fait représentées par un couple (lat, lon) où lat est la latitude de l'adresse et lon est la longitude de l'adresse. Par exemple, le 7 rue St-Hilaire à Toulouse est représenté par le couple (43.61319, 1.44209).

On souhaite rédiger un programme qui, à une adresse donnée (donc un couple latitude et longitude), indique quel est son lycée de secteur, en se basant sur le lycée de secteur de ses voisins.

La liste d'association est stockée sous la forme d'un dictionnaire nommé adresses_lycees. Voici ci-dessous un extrait de cette liste d'association. Le fichier complet vous sera donné plus tard.

1
adresses_lycees = {
2
    (43.116227, 0.718689): "Lycée Bagatelle",
3
    (43.592111, 1.459428): "Lycée Marcelin Berthelot",
4
    (43.587685, 1.48444): "Lycée Saint-Sernin",
5
    ...
6
}

On rappelle quelques opérations élémentaires sur les dictionnaires :

1
for adresse in adresses_lycees:  # Permet de parcourir uniquement les adresses existantes, stockées en temps que couple de données.
2
for (lat, lon) in assoc:  # Idem en obtenant directement les valeurs lat et lon au lieu d'un couple (lat, lon).
3
4
(lat, lon) in assoc  # Renvoie True si l'adresse existe dans le dictionnaire, False sinon
5
6
lycee = assoc[(lat, long)]  # Enregistre dans la variable lycee le nom du lycée associé à une adresse existante
7
lycee = assoc[adresse]  # Idem avec adresse un couple de coordonnées (lat, lon)
Toutes vos réponses sont à rédiger dans un fichier lycee_de_secteur.py et les tests présents dans les docstrings peuvent être exécutés en plaçant le code suivant dans votre fichier :
1
if __name__ == '__main__':
2
    # Tests des fonctions pouvant être testées avec doctest.
3
    # Il ne doit pas y avoir de failure dans l'exécution finale.
4
    import doctest
5
    doctest.testmod()
Question
Rédiger une fonction distance(lat_1, lon_1, lat_2, lon_2) qui renvoie la distance euclidienne entre deux points (lat_1, lon_1) et (lat_2, lon_2).
1
def distance(lat_1, lon_1, lat_2, lon_2):
2
    """
3
    Calcule la distance euclidienne entre deux points.
4
    :param lat_1: Latitude du point 1
5
    :param lon_1: Longitude du point 1
6
    :param lat_2: Latitude du point 2
7
    :param lon_2: Longitude du point 2
8
    >>> distance(43.57801, 1.44627, 43.59577, 1.45256)
9
    0.018840958043584093
10
    >>> distance(43.61125, 1.34041, 43.55486, 1.54005)
11
    0.2074511067697639
12
    """
13
    pass	
Indice
On rappelle la formule de la distance euclidienne : \(distance(A, B)=\sqrt{(x_A-x_B)^2+(y_A-y_B)^2}\)
Indice
Il faut importer la fonction sqrt depuis le module math :
1
from math import sqrt
2
3
# Utilisation :
4
sqrt(4)  # 2
Indice
Nos valeurs A et B dans la formule s'appliquent de cette façon :
  • \(x_A \rightarrow\) lat_1
  • \(x_B \rightarrow\) lat_2
  • \(y_A \rightarrow\) lon_1
  • \(y_B \rightarrow\) lon_2
Solution
1
from math import sqrt
2
3
4
def distance(lat_1, lon_1, lat_2, lon_2):
5
    """
6
    Calcule la distance euclidienne entre deux points.
7
    :param lat_1: Latitude du point 1
8
    :param lon_1: Longitude du point 1
9
    :param lat_2: Latitude du point 2
10
    :param lon_2: Longitude du point 2
11
    >>> distance(43.57801, 1.44627, 43.59577, 1.45256)
12
    0.018840958043584093
13
    >>> distance(43.61125, 1.34041, 43.55486, 1.54005)
14
    0.2074511067697639
15
    """
16
    diff_lat = (lat_2 - lat_1) ** 2
17
    diff_lon = (lon_2 - lon_1) ** 2
18
    return sqrt(diff_lat + diff_lon)
Où se trouvent nos données ?
Pour cet exercice, le dictionnaire contenant les données est déjà présent dans le fichier ci-joint :
donnees_lycees.py [py]
On peut l'importer en le plaçant dans le même dossier que le fichier Python de cet exercice, et en indiquant dans votre fichier de travail le code suivant :
1
from donnees_lycees import adresses_lycees
La première valeur donnees_lycees correspond au nom du fichier sans l'extension .py et la deuxième adresses_lycees correspond au nom du dictionnaire dans le fichier.
Question
On souhaite ensuite rédiger une fonction plus_proche(lat, lon, k, assoc) qui renvoie la liste des k plus proches adresses de (lat, lon) dans le dictionnaire assoc.
On propose pour cela l'algorithme suivant :
  • Stocker dans une liste distances l'ensemble des adresses et de leur distance à (lat, lon) sous la forme (distance, adresse). (voir premier indice si pas compris)
    Cette liste va permettre d'indiquer, pour chaque adresse, quelle est sa distance avec notre point de calculer (lat, lon) passé en paramètre de la fonction.
  • Trier la liste distances. Comment trier rapidement ?
    • Cela fonctionne car lorsqu'on trie une liste de tuples, le tri va se faire en priorité sur le premier élément du tuple (ici sur la distance). Ingénieux !
  • Parcourir les k premiers éléments de la liste distances et conserver les adresses dans une autre liste plus_proches. (voir deuxième indice si vous êtes vraiment perdus)
Rédiger cet algorithme en Python.
1
def plus_proche(lat, lon, k, assoc):
2
    """
3
    Renvoie les k plus proches adresses de (lat, lon)
4
    :param lat: Latitude de l'adresse
5
    :param lon: Longitude de l'adresse
6
    :param k: Nombre de voisins à renvoyer
7
    :param assoc: Dictionnaire qui associe un lycée à chaque adresse
8
    >>> plus_proche(43.61125, 1.34041, 8, adresses_lycees)
9
    [(43.61036, 1.33953), (43.609972, 1.340423), (43.61024, 1.34149), (43.609475, 1.340495), (43.609555, 1.339555), (43.613156, 1.340015), (43.61281, 1.339055), (43.610095, 1.338595)]
10
    >>> plus_proche(43.59577, 1.45256, 5, adresses_lycees)
11
    [(43.597102, 1.45326), (43.596568, 1.454731), (43.598, 1.453246), (43.597306, 1.450786), (43.595723, 1.454907)]
12
    """
13
    pass
Indice
On souhaite obtenir une liste qui ressemble à cela :
1
distances = [(0.3, (43.52791, 1.23712)), (0.2, (43.21831, 1.63139))]
Cette liste a deux éléments :
  • Le premier est l'adresse (43.52791, 1.23712) située à distance 0.3 de l'adresse fournie en paramètre de la fonction (lat, lon)
  • Le second est l'adresse (43.21831, 1.63139) située à distance 0.2 de l'adresse fournie en paramètre de la fonction (lat, lon)
Pour y parvenir, il faut :
  • parcourir toutes les adresses de assoc (par exemple avec for (lat_1, lon_1) in assoc:) ;
  • calculer la distance d avec (lat, lon) ;
  • l'ajouter dans la liste distances sous la forme (d, (lat_1, lon_1))
Indice
Il suffit de parcourir les indices de 0 à k (exclu) en utilisant la boucle FOR et range(k).
Si on utilise i comme variant de notre boucle for, on peut ensuite récupérer l'adresse avec distances[i][1].
  • Pourquoi 1 ? Parce-que distances[i] est un tuple qui contient comme premier élément la distance, et comme deuxième élément l'adresse.
Solution
1
def plus_proche(lat, lon, k, assoc):
2
    """
3
    Renvoie les k plus proches adresses de (lat, lon)
4
    :param lat: Latitude de l'adresse
5
    :param lon: Longitude de l'adresse
6
    :param k: Nombre de voisins à renvoyer
7
    :param assoc: Dictionnaire qui associe un lycée à chaque adresse
8
    >>> plus_proche(43.61125, 1.34041, 8, adresses_lycees)
9
    [(43.61036, 1.33953), (43.609972, 1.340423), (43.61024, 1.34149), (43.609475, 1.340495), (43.609555, 1.339555), (43.613156, 1.340015), (43.61281, 1.339055), (43.610095, 1.338595)]
10
    >>> plus_proche(43.59577, 1.45256, 5, adresses_lycees)
11
    [(43.597102, 1.45326), (43.596568, 1.454731), (43.598, 1.453246), (43.597306, 1.450786), (43.595723, 1.454907)]
12
    """
13
    distances = []  # Contient des éléments sous la forme (d, (lat, lon))
14
    # Parcours de toutes les adresses existantes
15
    for lat_1, lon_1 in assoc:
16
        d = distance(lat, lon, lat_1, lon_1)
17
        distances.append((d, (lat_1, lon_1)))
18
19
    # Tri des distances
20
    distances.sort()
21
22
    # Sauvegarde des k plus proches
23
    plus_proches = []
24
    for i in range(k):
25
        plus_proches.append(distances[i][1])
26
27
    return plus_proches
On approche de la fin
Plus que quelques lignes de code et on pourra connaître le lycée de secteur de n'importe qui en Haute-Garonne !
Il ne reste plus qu'à exploiter les résultats, le plus dur est déjà derrière vous ! Dans la dernière fonction de votre programme, vous allez devoir déterminer quel est le lycée de secteur d'une adresse donnée.
Question
Rédiger une fonction lycee_de_secteur(lat, lon) qui renvoie le nom du lycée de secteur d'une adresse donnée en paramètre.
Vous êtes libres de choisir la valeur qui vous semble la plus appropriée pour k en paramètre par défaut.
On utilisera max(liste, key=liste.count) pour connaître la valeur de l'élément le plus fréquent dans la liste liste. (le deuxième indice vous explique comment ça marche)
Le premier indice déroule l'algorithme à coder en Python.
1
def lycee_de_secteur(lat, lon, k=5):
2
    """
3
    Renvoie le nom du lycée de secteur depuis une adresse
4
    :param lat: Latitude de l'adresse
5
    :param lon: Longitude de l'adresse
6
    :param k: Nombre de voisins à prendre en compte
7
    >>> lycee_de_secteur(43.62225, 1.39855, 5)
8
    'Lycée Saint-Exupéry'
9
    >>> lycee_de_secteur(43.46647, 1.06295, 10)
10
    'Lycée Charles de Gaulle'
11
    """
12
    pass
Indice
Voici le déroulé de notre algorithme :
  • Récupérer la liste des plus proches voisins grâce à la fonction précédemment codée.
    • Vous pouvez choisir la valeur de k que vous souhaitez en paramètre par défaut (par exemple 5).
    • Vous devez utiliser adresses_lycees pour le paramètre assoc de plus_proche().
  • Créer une liste lycees qui contient tous les lycées de secteur de nos voisins.
    • Vous devrez parcourir tous les plus proches voisins (obtenus avec l'étape précédente).
    • Pour chaque voisin, on peut récupérer son lycée de secteur grâce à adresses_lycees[voisin].
  • Rechercher et renvoyer la valeur la plus fréquente dans la liste lycees.
Indice
On peut obtenir la valeur la plus fréquente dans une liste grâce à max(liste, key=liste.count). Pourquoi ?
  • La fonction max() renvoie la valeur la plus grande dans une liste (ex : max([2,5,3]) renvoie 5).
  • Le paramètre key= permet de précisier une fonction a utiliser sur chaque élément avant de le comparer aux autres.
  • La fonction liste.count renvoie le nombre d'occurences d'un élément passé en paramètre.
    • Les parenthèses ne sont d'ailleurs pas présentes car on ne veut pas donner à max() le résultat de la fonction, mais le nom de la fonction qu'il devra utiliser.
Donc la fonction max() regarde le nombre d'occurences de chaque élément, et pour celui dont cette valeur est la plus élevée, va renvoyer sa valeur.
Solution
1
def lycee_de_secteur(lat, lon, k=5):
2
    """
3
    Renvoie le nom du lycée de secteur depuis une adresse
4
    :param lat: Latitude de l'adresse
5
    :param lon: Longitude de l'adresse
6
    :param k: Nombre de voisins à prendre en compte
7
    >>> lycee_de_secteur(43.62225, 1.39855, 5)
8
    'Lycée Saint-Exupéry'
9
    >>> lycee_de_secteur(43.46647, 1.06295, 10)
10
    'Lycée Charles de Gaulle'
11
    """
12
    plus_proches = plus_proche(lat, lon, k, adresses_lycees)
13
14
    # On stocke le nom des lycées de secteur de chaque voisin
15
    lycees = []
16
    for voisin in plus_proches:
17
        lycees.append(adresses_lycees[voisin])
18
19
    # On renvoie le lycée le plus fréquent
20
    return max(lycees, key=lycees.count)
Pour les plus rapides
Si vous avez tout terminé, bravo ! Le reste des exercices n'est que du bonus, et n'est pas à connaître. Il s'agit de deux questions bonus :
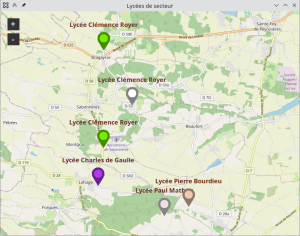
  • La première consiste à créer une carte sur laquelle apparaissent les voisins d'une couleur différente selon leur lycée de secteur.
  • La seconde consiste à revoir la fonction de distance pour calculer correctement la distance entre deux adresses géographiques.
Question
Ce premier exercice consiste donc à obtenir le résultat ci-contre.
On doit pouvoir afficher les voisins autour de nous, avec le nom de leur lycée de secteur.
On utilisera pour cela le module TkinterMapView. Il est déjà installé sur les ordinateurs du lycée. Chez vous, il faudra taper pip3 install tkintermapview dans le terminal.
On dispose également de deux couleurs associées à chaque lycée, toujours dans le fichier donnees_lycees où couleurs_lycees est un dictionnaire qui à chaque lycée associe deux couleurs dans un tuple.
1
from donnees_lycees import adresses_lycees, couleurs_lycees
Compléter la fonction ci-dessous pour afficher les points sur la carte.
1
from tkinter import Tk
2
from tkintermapview import TkinterMapView
3
4
def afficher_voisins(lat, lon, k=10):
5
    # Création de la fenetre Tkinter
6
    largeur, hauteur = 800, 600
7
    fenetre = Tk(
8
)
9
    fenetre.geometry(f"{largeur}x{hauteur}")
10
    fenetre.title("Lycées de secteur")
11
12
    # Ajout de la carte à la fenêtre
13
    carte = TkinterMapView(fenetre, width=largeur, height=hauteur, corner_radius=0)
14
    carte.place(relx=0.5, rely=0.5, anchor=CENTER)
15
16
    # On récupère les lycées les plus proches
17
    plus_proches = ...
18
19
    # On ajoute les voisins à la carte
20
    for lat_voisin, lon_voisin in plus_proches:
21
        # On récupère toutes les infos pour l'affichage
22
        lycee = ....
23
        couleur_1, couleur_2 = ...
24
25
        # On affiche le voisin
26
        carte.set_marker(lat_voisin, lon_voisin, text=lycee, marker_color_circle=couleur_1, marker_color_outside=couleur_2)
27
28
    # On ajoute l'adresse de recherche sur la carte avec le lycée final
29
    carte.set_position(lat, lon, marker=True, text=lycee_de_secteur(lat, lon, k), marker_color_circle="white", marker_color_outside="gray")
30
    carte.set_zoom(16)
31
32
    # On affiche la carte
33
    carte.mainloop()
Solution
1
def afficher_voisins(lat, lon, k=10):
2
    # Création de la fenetre Tkinter
3
    largeur, hauteur = 800, 600
4
    fenetre = Tk()
5
    fenetre.geometry(f"{largeur}x{hauteur}")
6
    fenetre.title("Lycées de secteur")
7
8
    # Ajout de la carte à la fenêtre
9
    carte = TkinterMapView(fenetre, width=largeur, height=hauteur, corner_radius=0)
10
    carte.place(relx=0.5, rely=0.5, anchor=CENTER)
11
12
    # On récupère les lycées les plus proches
13
    plus_proches = plus_proche(lat, lon, k, adresses_lycees)
14
15
    # On ajoute les voisins à la carte
16
    for lat_voisin, lon_voisin in plus_proches:
17
        # On récupère toutes les infos pour l'affichage
18
        lycee = adresses_lycees[(lat_voisin, lon_voisin)]
19
        couleur_1, couleur_2 = couleurs_lycees[lycee]
20
21
        # On affiche le voisin
22
        carte.set_marker(lat_voisin, lon_voisin, text=lycee, marker_color_circle=couleur_1, marker_color_outside=couleur_2)
23
24
    # On ajoute l'adresse de recherche sur la carte avec le lycée final
25
    carte.set_position(lat, lon, marker=True, text=lycee_de_secteur(lat, lon, k), marker_color_circle="white", marker_color_outside="gray")
26
    carte.set_zoom(16)
27
28
    # On affiche la carte
29
    carte.mainloop()
Question
Ce deuxième exercice consiste à réécrire la fonction distance() en prenant en compte la courbure de la Terre et en calculant la vraie distance en km entre deux points géographiques.
Cette distance est appelée formule de haversine et s'applique à toute sphère. La formule est donnée ci-dessous :
\(d = 2 r \arcsin\left(\sqrt{\sin^2\left(\frac{x_2 - x_1}{2}\right) + \cos(x_1) \cos(x_2)\sin^2\left(\frac{y_2 - y_1}{2}\right)}\right)\)
  • où \(r\) est le rayon de la sphère (6371 km)
  • \((x_1, y_1)\) correspond au premier point
  • \((x_2, y_2)\) correspond au second point
Attention, les coordonnées sont à représenter en radians. Il faudra donc d'abord transformer les différentes coordonnées (exprimées en degrés) en radians.
Vous aurez aussi besoin d'importer quelques fonctions depuis le module math :
1
from math import sin, cos, atan2, sqrt, pi
Rédiger la fonction distance_km(lat1, lon1, lat2, lon2) qui implémente cette fonction de haversine.
1
def distance_km(lat1, lon1, lat2, lon2):
2
    """
3
    Calcule la distance de haversine entre deux points.
4
    :param lat_1: Latitude du point 1
5
    :param lon_1: Longitude du point 1
6
    :param lat_2: Latitude du point 2
7
    :param lon_2: Longitude du point 2
8
    >>> distance_km(43.57801, 1.44627, 43.59577, 1.45256)
9
    2.0387675154222005
10
    >>> distance_km(43.61125, 1.34041, 43.55486, 1.54005)
11
    17.259635893940143
12
    """
13
    pass
Indice
Pour traduire les degrés en radians, on pourra utiliser le code suivant :
1
def deg2rad(deg):
2
    return deg * (pi / 180)
Solution
1
def deg2rad(deg):
2
    return deg * (pi / 180)
3
4
def distance_km(lat1, lon1, lat2, lon2):
5
    """
6
    Calcule la distance de haversine entre deux points.
7
    :param lat_1: Latitude du point 1
8
    :param lon_1: Longitude du point 1
9
    :param lat_2: Latitude du point 2
10
    :param lon_2: Longitude du point 2
11
    >>> distance_km(43.57801, 1.44627, 43.59577, 1.45256)
12
    2.0387675154222005
13
    >>> distance_km(43.61125, 1.34041, 43.55486, 1.54005)
14
    17.259635893940143
15
    """
16
    R = 6371
17
    dLat = deg2rad(lat2 - lat1)
18
    dLon = deg2rad(lon2 - lon1)
19
    a = sin(dLat / 2) * sin(dLat / 2) + cos(deg2rad(lat1)) * cos(deg2rad(lat2)) * sin(dLon / 2) * sin(dLon / 2)
20
    c = atan2(sqrt(a), sqrt(1 - a))
21
    d = 2 * R * c
22
    return d