Transcodage : changement de base
Transcodage : depuis toutes les bases vers le décimal
Définition :
Passer de l'écriture en base b d'un nombre à son écriture décimale est aisé, il suffit de faire la somme de la multiplication de chaque chiffre d'indice k par son poids correspondant bk (b étant la base d'origine).
Exemple : Hexadécimal vers Décimal
On préalable, on prendra soin de transcoder les lettres A à F en décimal (de 10 à 15) :
A vaut 10
B vaut 11
C vaut 12
D vaut 13
E vaut 14
F vaut 15.
(FA9)16= 15 x 162 + 10 x 161 + 9 x 160 = 3840 + 160 + 9 = (4009)10
Transcodage : depuis le décimal vers les autres bases
Méthode :
Pour convertir un nombre (N)10 écrit en base 10 dans la base b, il faut effectuer des divisions euclidiennes successives, d'abord de N par b puis des quotients obtenus par b jusqu'à ce que le quotient soit 0. Les restes successifs sont ensuite écrits du dernier au premier de gauche à droite.
Rappel : Division euclidienne
a et b sont deux entiers naturels, avec b non nul. On appelle division euclidienne de a par b la division donnant un quotient et un reste entiers tels que 0 ⩽ r < b .
Cette division « entière » conduit à l'égalité : a = b x q + r
Ainsi, on aura un reste égal à 0 ou 1 si on transcode en binaire, ou un reste compris entre 0 et 15 si on transcode en hexadécimal.
En Python, on obtient :
le quotient de a par b avec l'instruction : q = a // b
le reste de a par b avec l'instruction : r = a % b
Exemple : Décimal vers Binaire
Ainsi, si on veut trouver un résultat en binaire, on va diviser par 2. Si on veut de l'hexadécimal, on va diviser par 16.
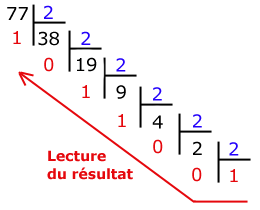
Le résultat sera donc (77)10 = (1001101)2 (lecture de bas vers le haut des restes)